§ 3. Перпендикулярність у просторі » 14.33

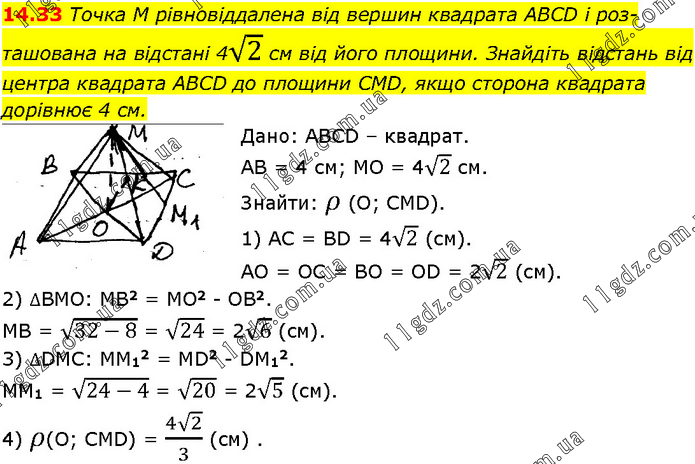
Точка M рівновіддалена від вершин квадрата ABCD і роз- ташована на відстані 4√2 см від його площини. Знайдіть відстань від центра квадрата ABCD до площини CMD, якщо сторона квадрата дорівнює 4 см. Дано: АВСD – квадрат. АВ = 4 см; МО = 4√2 см. Знайти: ρ (О; СМD). 1) АС = ВD = 4√2 (см). АО = ОС = ВО = ОD = 2√2 (см). 2) ∆ВМО: МВ2 = МО2 - ОВ2. МВ = √(32-8) = √24 = 2√6 (см). 3) ∆DМС: ММ12 = МD2 - DМ12. ММ1 = √(24-4) = √20 = 2√5 (см). 4) ρ(О; СМD) = (4√2)/3 (см) .