§ 3. Перпендикулярність у просторі » 14.30

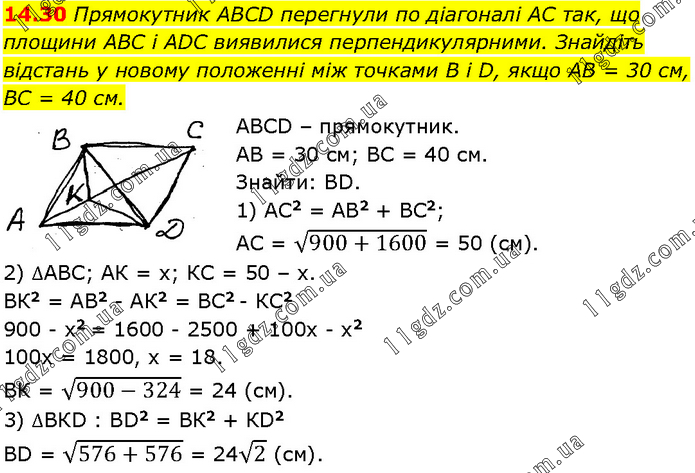
Прямокутник ABCD перегнули по діагоналі AC так, що площини ABC і ADC виявилися перпендикулярними. Знайдіть відстань у новому положенні між точками B і D, якщо AB = 30 см, BC = 40 см. АВСD – прямокутник. АВ = 30 см; ВС = 40 см. Знайти: ВD. 1) АС2 = АВ2 + ВС2; АС = √(900+1600) = 50 (см). 2) ∆АВС; АК = х; КС = 50 – х. ВК2 = АВ2 - АК2 = ВС2 - КС2 900 - х2 = 1600 - 2500 + 100х - х2 100х = 1800, х = 18. ВК = √(900-324) = 24 (см). 3) ∆ВКD : ВD2 = ВК2 + КD2 ВD = √(576+576) = 24√2 (см).