Розділ 3. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ » 9.16

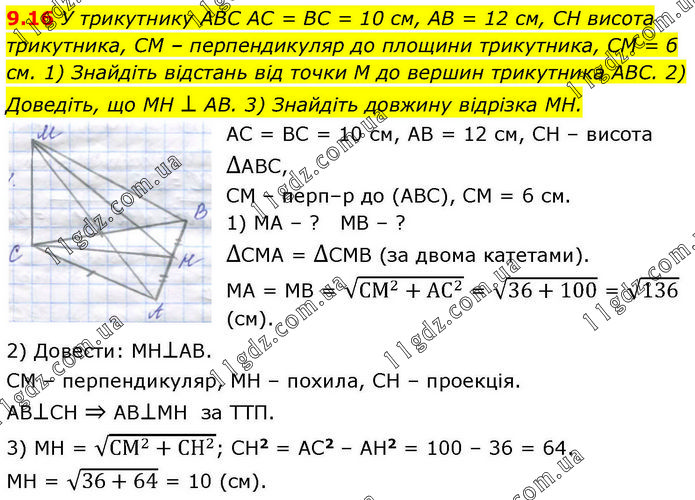
У трикутнику ABC AC = BC = 10 см, AB = 12 см, CH висота трикутника, CM – перпендикуляр до площини трикутника, CM = б см. 1) Знайдіть відстань від точки M до вершин трикутника ABC. 2) Доведіть, що MH ⊥ AB. 3) Знайдіть довжину відрізка MH. АС = ВС = 10 см, АВ = 12 см, СН – висота ∆АВС, СМ – перп–р до (АВС), СМ = 6 см. 1) МА – ? МВ – ? ∆СМА = ∆СМВ (за двома катетами). МА = МВ = √(СМ^2+АС^2 ) = √(36+100) = √136 (см). 2) Довести: МН⊥АВ. СМ – перпендикуляр, МН – похила, СН – проекція. АВ⊥СН ⇒ АВ⊥МН за ТТП. 3) МН = √(СМ^2+СН^2 ); СН2 = АС2 – АН2 = 100 – 36 = 64. МН = √(36+64) = 10 (см).