Розділ 3. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ » 12.74

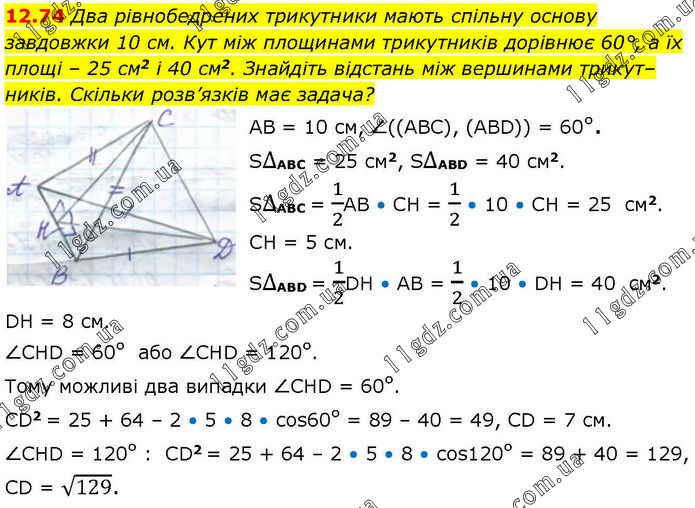
Два рівнобедрених трикутники мають спільну основу завдовжки 10 см. Кут між площинами трикутників дорівнює 60°, а їх площі – 25 см2 і 40 см2. Знайдіть відстань між вершинами трикут–ників. Скільки розв’язків має задача? АВ = 10 см, ∠((АВС), (АВD)) = 60°. S∆АВС = 25 см2, S∆АВD = 40 см2. S∆АВС = 1/2АВ • СН = 1/2 • 10 • СН = 25 см2. СН = 5 см. S∆АВD = 1/2DН • АВ = 1/2 • 10 • DН = 40 см2. DН = 8 см. ∠СНD = 60° або ∠СНD = 120°. Тому можливі два випадки ∠СНD = 60°. СD2 = 25 + 64 – 2 • 5 • 8 • cos60° = 89 – 40 = 49, CD = 7 см. ∠СНD = 120° : СD2 = 25 + 64 – 2 • 5 • 8 • cos120° = 89 + 40 = 129, CD = √129.