Розділ 3. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ » 8.35

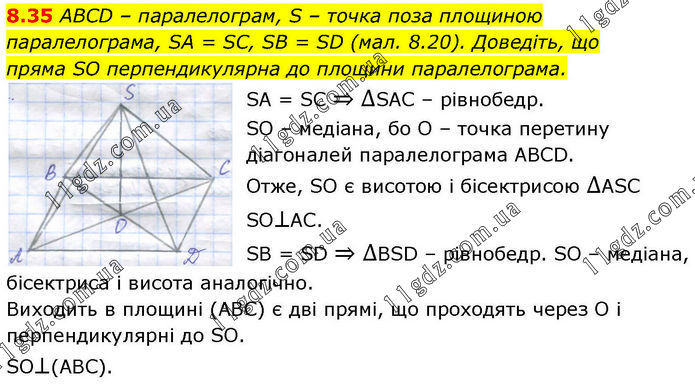
ABCD – паралелограм, S – точка поза площиною паралелограма, SA = SC, SB = SD (мал. 8.20). Доведіть, що пряма SO перпендикулярна до площини паралелограма. SA = SC ⇒ ∆SAC – рівнобедр. SO – медіана, бо О – точка перетину діагоналей паралелограма АВСD. Отже, SO є висотою і бісектрисою ∆АSC SO⊥AC. SB = SD ⇒ ∆BSD – рівнобедр. SO – медіана, бісектриса і висота аналогічно. Виходить в площині (АВС) є дві прямі, що проходять через О і перпендикулярні до SO. SO⊥(ABC).