Розділ 3. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ » 11.56

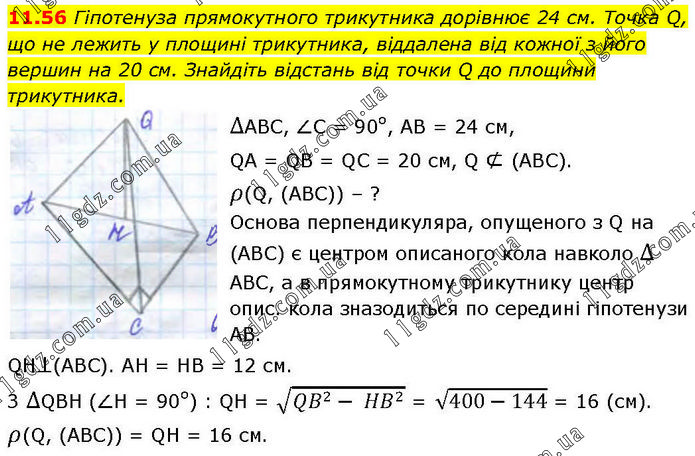
Гіпотенуза прямокутного трикутника дорівнює 24 см. Точка Q, що не лежить у площині трикутника, віддалена від кожної з його вершин на 20 см. Знайдіть відстань від точки Q до площини трикутника. ∆АВС, ∠С = 90°, АВ = 24 см, QA = QB = QC = 20 см, Q ⊄ (ABC). ρ(Q, (ABC)) – ? Основа перпендикуляра, опущеного з Q на (АВС) є центром описаного кола навколо ∆ АВС, а в прямокутному трикутнику центр опис. кола зназодиться по середині гіпотенузи АВ. QH⊥(ABC). AH = HB = 12 см. З ∆QBH (∠H = 90°) : QH = √(QB^2- HB^2 ) = √(400-144) = 16 (см). ρ(Q, (ABC)) = QH = 16 см.