Розділ 2. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ » 7.24

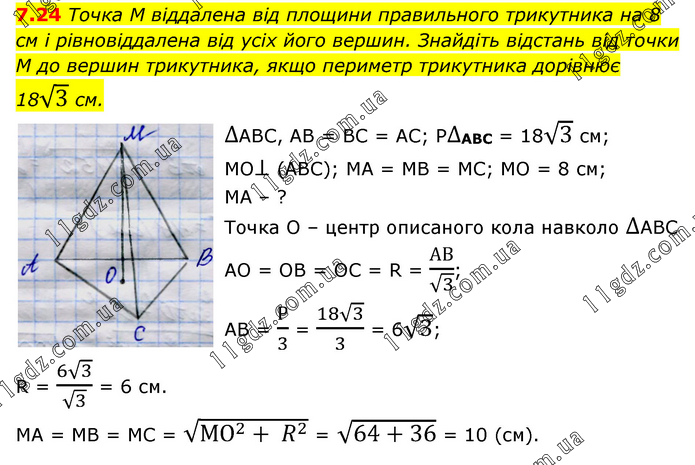
Точка М віддалена від площини правильного трикутника на 8 см і рівновіддалена від усіх його вершин. Знайдіть відстань від точки М до вершин трикутника, якщо периметр трикутника дорівнює 18√3 см. ∆АВС, АВ = ВС = АС; Р∆АВС = 18√3 см; МО⊥ (АВС); МА = МВ = МС; МО = 8 см; МА – ? Точка О – центр описаного кола навколо ∆АВС АО = ОВ = ОС = R = АВ/√3; АВ = Р/3 = (18√3)/3 = 6√3; R = (6√3)/√3 = 6 см. МА = МВ = МС = √(МО^2+ R^2 ) = √(64+36) = 10 (см).