Розділ 2. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ » 6.37

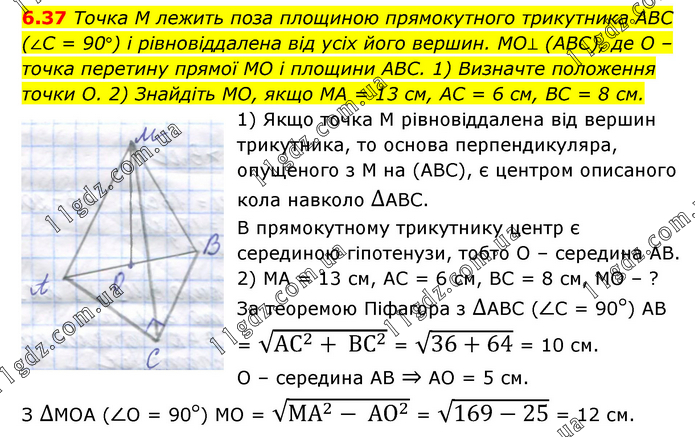
Точка М лежить поза площиною прямокутного трикутника АВС (∠С = 90°) і рівновіддалена від усіх його вершин. МО⊥ (АВС), де О – точка перетину прямої МО і площини АВС. 1) Визначте положення точки О. 2) Знайдіть МО, якщо МА = 13 см, АС = 6 см, ВС = 8 см. 1) Якщо точка М рівновіддалена від вершин трикутника, то основа перпендикуляра, опущеного з М на (АВС), є центром описаного кола навколо ∆АВС. В прямокутному трикутнику центр є серединою гіпотенузи, тобто О – середина АВ. 2) МА = 13 см, АС = 6 см, ВС = 8 см, МО – ? За теоремою Піфагора з ∆АВС (∠С = 90°) АВ = √(АС^2+ ВС^2 ) = √(36+64) = 10 см. О – середина АВ ⇒ АО = 5 см. З ∆МОА (∠О = 90°) МО = √(МА^2- АО^2 ) = √(169-25) = 12 см.