Розділ 2. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ » 6.36

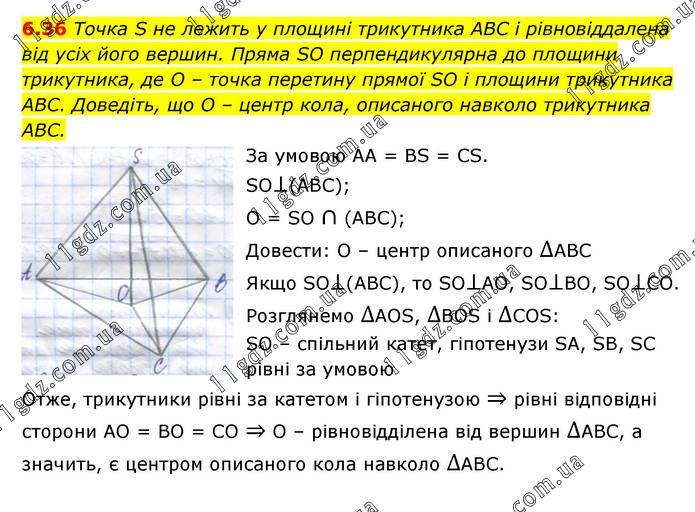
Точка S не лежить у площині трикутника АВС і рівновіддалена від усіх його вершин. Пряма SО перпендикулярна до площини трикутника, де О – точка перетину прямої SО і площини трикутника АВС. Доведіть, що О – центр кола, описаного навколо трикутника АВС. За умовою АA = BS = CS. SO⊥(ABC); O = SO ∩ (ABC); Довести: О – центр описаного ∆АВС Якщо SO⊥(ABC), то SO⊥AO, SO⊥BO, SO⊥CO. Розглянемо ∆АОS, ∆ВОS і ∆СОS: SО – спільний катет, гіпотенузи SА, SВ, SС рівні за умовою Отже, трикутники рівні за катетом і гіпотенузою ⇒ рівні відповідні сторони АО = ВО = СО ⇒ О – рівновідділена від вершин ∆АВС, а значить, є центром описаного кола навколо ∆АВС.