ГДЗ / ГДЗ Математика 10 клас Істер 2018 / Розділ 2. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ / 9.7

Розділ 2. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ » 6.47



« 6.46
6.47
6.48 »

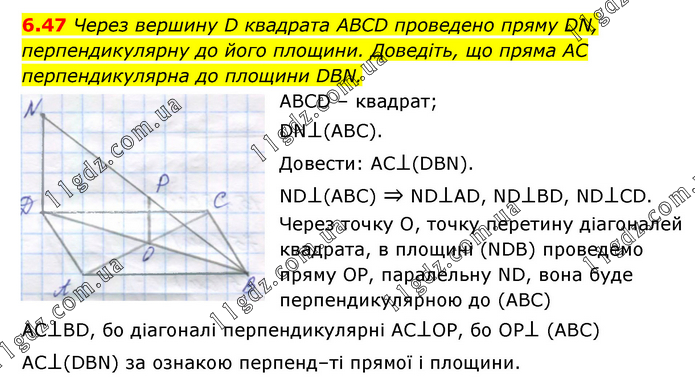
Через вершину D квадрата АВСD проведено пряму DN, перпендикулярну до його площини. Доведіть, що пряма АС перпендикулярна до площини DВN. АВСD – квадрат; DN⊥(АВС). Довести: АС⊥(DBN). ND⊥(ABC) ⇒ ND⊥AD, ND⊥BD, ND⊥CD. Через точку О, точку перетину діагоналей квадрата, в площині (NDB) проведемо пряму ОР, паралельну ND, вона буде перпендикулярною до (АВС) АС⊥ВD, бо діагоналі перпендикулярні АС⊥ОР, бо ОР⊥ (АВС) АС⊥(DВN) за ознакою перпенд–ті прямої і площини.

Повідомити про помилку


Розділ 2. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ

6.1-2
6.3-4
6.5-6
6.7
6.8
6.9 (1-3)
6.9 (4)
6.10
6.11-12
6.13
6.14
6.15
6.16 (1-3)
6.16 (4)
6.17 (1)
6.17 (2)
6.17 (3-4)
6.18-19
6.20
6.21
6.22
6.23
6.24
6.25
6.26
6.27
6.28
6.29
6.30
6.31
6.32
6.33
6.34-35
6.36
6.37
6.38
6.39
6.40
6.41
6.42
6.43
6.44
6.45
6.46
6.47
6.48
6.49
6.50-7.1
7.2
7.3
7.4-5
7.6
7.7
7.8
7.9
7.10
7.11
7.12
7.13
7.14
7.15
7.16
7.17
7.18
7.19
7.20
7.21
7.22
7.23
7.24
7.25
7.26
7.27
7.28
7.29
7.30
7.31
7.32
7.33
7.34
7.35
7.36
7.37-38
7.39
7.40
7.41
7.42
7.43
7.44
7.45
7.46
7.47
7.48
7.49
7.50
7.51
7.52
8.3-5
8.6-7
8.9
8.10
8.11
8.12
8.13
8.14
8.15
8.16
8.17
8.18
8.19
8.20
8.21
8.22
8.23
8.24
8.25
8.26
8.27
8.28
8.29
8.30
8.31
8.32
8.33
8.34
8.35
8.36
8.37
8.38
8.39
8.40
8.41
8.42
8.43
9.1-2
9.3
9.4
9.5
9.6
9.7
9.8
9.9
9.10
9.11
9.12
9.13
9.14
9.15
9.16
9.17
9.18
9.19
9.20
9.21
9.22
9.23
9.24
9.25
9.26
9.27
9.28
9.29
9.30
9.31
9.32
9.33
9.34
9.35
9.36
9.37
9.38
10.3-6
10.8
10.9
10.10
10.11
10.13
10.15
10.16-17
10.18-19
10.20
10.21
10.22
10.23
10.24
10.25
10.26
10.27
10.28
10.29-31
10.32
10.33
10.34
10.35
10.36
10.37
10.38
10.39
10.40
10.41
10.42
10.43
10.44
10.45
10.46
10.47-48
10.49-50