Розділ 2. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ » 9.22

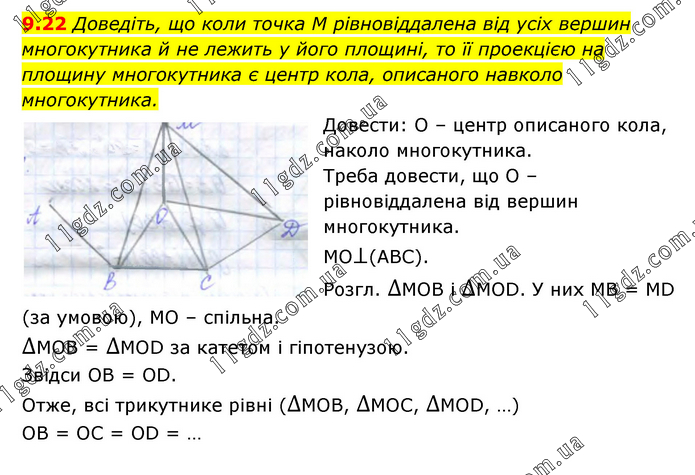
Доведіть, що коли точка М рівновіддалена від усіх вершин многокутника й не лежить у його площині, то її проекцією на площину многокутника є центр кола, описаного навколо многокутника. Довести: О – центр описаного кола, наколо многокутника. Треба довести, що О – рівновіддалена від вершин многокутника. МО⊥(АВС). Розгл. ∆МОВ і ∆МОD. У них МВ = МD (за умовою), МО – спільна. ∆МОВ = ∆МОD за катетом і гіпотенузою. Звідси ОВ = ОD. Отже, всі трикутнике рівні (∆МОВ, ∆МОС, ∆МОD, …) ОВ = ОС = ОD = …