Розділ 2. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ » 9.25
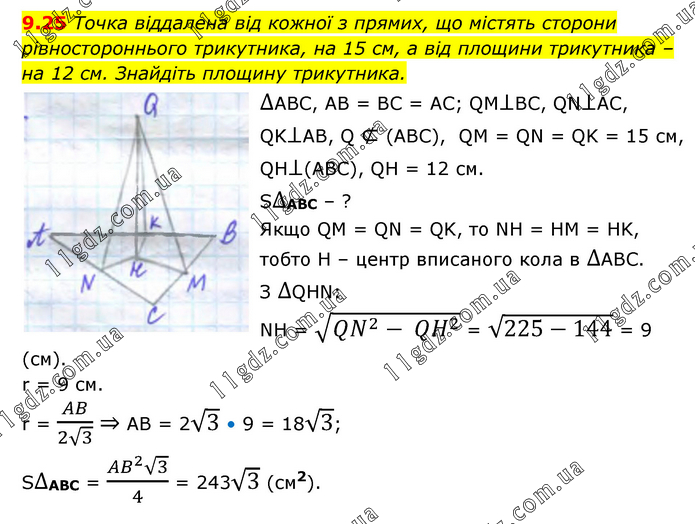
Точка віддалена від кожної з прямих, що містять сторони рівностороннього трикутника, на 15 см, а від площини трикутника – на 12 см. Знайдіть площину трикутника. ∆ABC, AB = BC = AC; QM⊥BC, QN⊥AC, QK⊥AB, Q ⊄ (ABC), QM = QN = QK = 15 см, QH⊥(ABC), QH = 12 см. S∆ABC – ? Якщо QM = QN = QK, то NH = HM = HK, тобто H – центр вписаного кола в ∆АВС. З ∆QHN: NH = √(QN^2- QH^2 ) = √(225-144) = 9 (cм). r = 9 cм. r = AB/(2√3) ⇒ AB = 2√3 • 9 = 18√3; S∆ABC = (AB^2 √3)/4 = 243√3 (см2).