Розділ 2. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ » 6.31

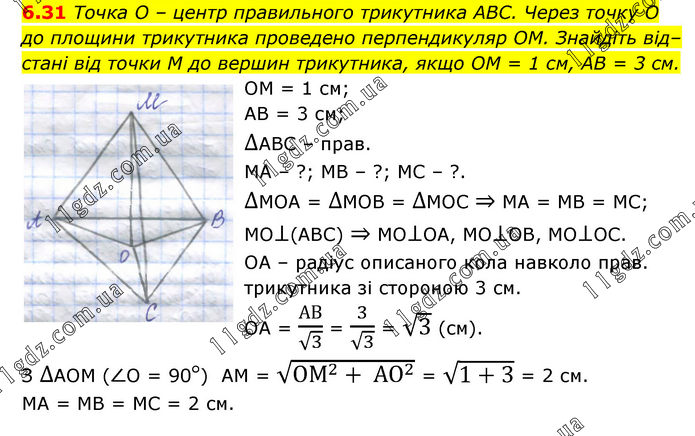
Точка О – центр правильного трикутника АВС. Через точку О до площини трикутника проведено перпендикуляр ОМ. Знайдіть від–стані від точки М до вершин трикутника, якщо ОМ = 1 см, АВ = 3 см. ОМ = 1 см; АВ = 3 см; ∆АВС – прав. МА – ?; МВ – ?; МС – ?. ∆МОА = ∆МОВ = ∆МОС ⇒ МА = МВ = МС; МО⊥(АВС) ⇒ МО⊥ОА, МО⊥ОВ, МО⊥ОС. ОА – радіус описаного кола навколо прав. трикутника зі стороною 3 см. ОА = АВ/√3 = 3/√3 = √3 (см). З ∆АОМ (∠О = 90°) АМ = √(ОМ^2+ АО^2 ) = √(1+3) = 2 см. МА = МВ = МС = 2 см.