Розділ 2. ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ » 10.27

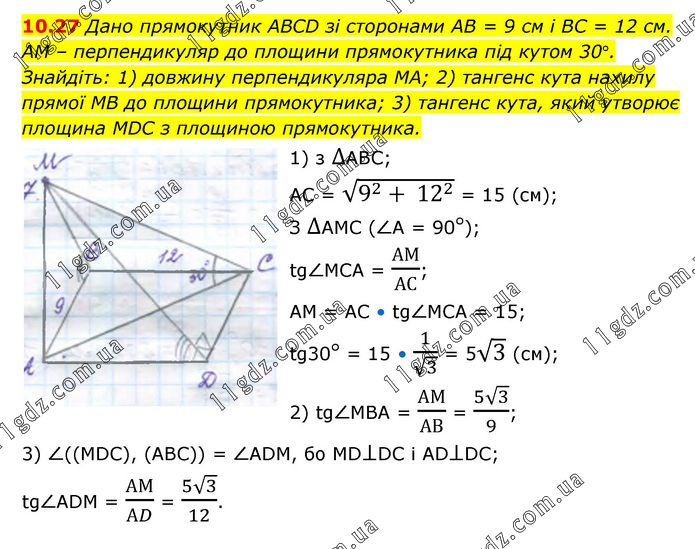
Дано прямокутник АВСD зі сторонами АВ = 9 см і ВС = 12 см. АМ – перпендикуляр до площини прямокутника під кутом 30°. Знайдіть: 1) довжину перпендикуляра МА; 2) тангенс кута нахилу прямої МВ до площини прямокутника; 3) тангенс кута, який утворює площина МDС з площиною прямокутника. 1) з ∆АВС; АС = √(9^2+ 12^2 ) = 15 (см); З ∆АМС (∠А = 90°); tg∠МСА = АМ/АС; АМ = АС • tg∠МСА = 15; tg30° = 15 • 1/√3 = 5√3 (см); 2) tg∠МВА = АМ/АВ = (5√3)/9; 3) ∠((МDС), (АВС)) = ∠АDМ, бо МD⊥DС і АD⊥DС; tg∠АDМ = АМ/АD = (5√3)/12.