§ 4. Координати та вектори в просторі » 20.34

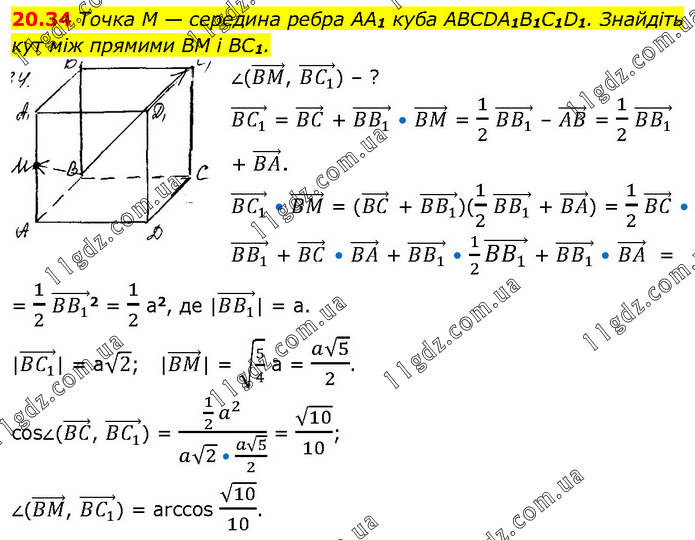
Точка M — середина ребра AA1 куба ABCDA1B1C1D1. Знайдіть кут між прямими BM і BC1. ∠((BM) ⃗, (BC_1 ) ⃗) – ? (BC_1 ) ⃗ = (BC) ⃗ + (BB_1 ) ⃗ • (BM) ⃗ = 1/2 (BB_1 ) ⃗ – (AB) ⃗ = 1/2 (BB_1 ) ⃗ + (BA) ⃗. (BC_1 ) ⃗ • (BM) ⃗ = ((BC) ⃗ + (BB_1 ) ⃗)(1/2 (BB_1 ) ⃗ + (BA) ⃗) = 1/2 (BC) ⃗ • (BB_1 ) ⃗ + (BC) ⃗ • (BA) ⃗ + (BB_1 ) ⃗ • 1/2 (BB_1 ) ⃗ + (BB_1 ) ⃗ • (BA) ⃗ = = 1/2 (BB_1 ) ⃗2 = 1/2 a2, де |(BB_1 ) ⃗| = a. |(BC_1 ) ⃗| = a√2; |(BM) ⃗| = √(5/4) a = (a√5)/2. cos∠((BC) ⃗, (BC_1 ) ⃗) = (1/2 a^2)/(a√2 • (a√5)/2) = √10/10; ∠((BM) ⃗, (BC_1 ) ⃗) = arccos √10/10.