§ 4. Координати та вектори в просторі » 19.35

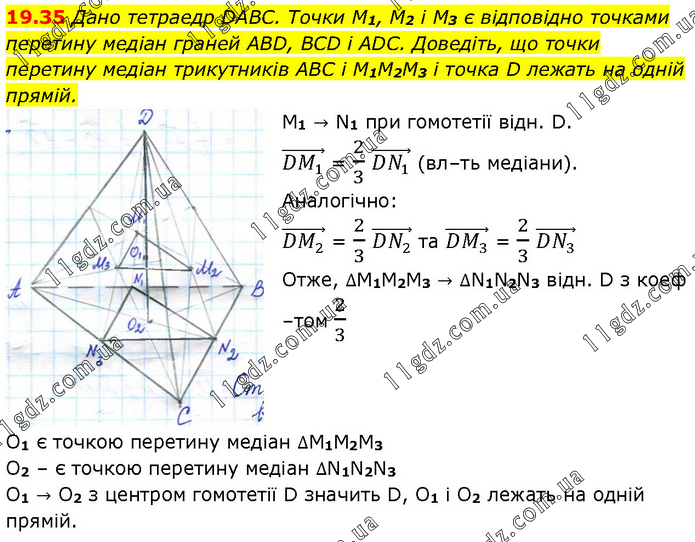
Дано тетраедр DABC. Точки M1, M2 і M3 є відповідно точками перетину медіан граней ABD, BCD і ADC. Доведіть, що точки перетину медіан трикутників ABC і M1M2M3 і точка D лежать на одній прямій. M1 → N1 при гомотетії відн. D. (DM_1 ) ⃗ = 2/3 (DN_1 ) ⃗ (вл–ть медіани). Аналогічно: (DM_2 ) ⃗ = 2/3 (DN_2 ) ⃗ та (DM_3 ) ⃗ = 2/3 (DN_3 ) ⃗ Отже, ∆М1М2М3 → ∆N1N2N3 відн. D з коеф –том 2/3 О1 є точкою перетину медіан ∆М1М2М3 О2 – є точкою перетину медіан ∆N1N2N3 О1 → О2 з центром гомотетії D значить D, O1 i O2 лежать на одній прямій.