§ 2. Паралельність у просторі » 5.15-5.16

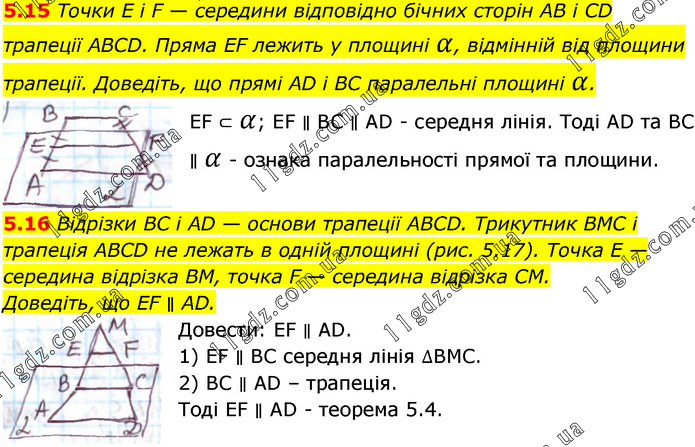
5.15 Точки E і F — середини відповідно бічних сторін AB і CD трапеції ABCD. Пряма EF лежить у площині α, відмінній від площини трапеції. Доведіть, що прямі AD і BC паралельні площині α. EF ⊂ α; EF ∥ BC ∥ AD - середня лінія. Тоді AD та ВС ∥ α - ознака паралельності прямої та площини. 5.16 Відрізки BC і AD — основи трапеції ABCD. Трикутник BMC і трапеція ABCD не лежать в одній площині (рис. 5.17). Точка E — середина відрізка BM, точка F — середина відрізка CM. Доведіть, що EF ∥ AD. Довести: EF ∥ AD. 1) EF ∥ BC середня лінія ∆ВМС. 2) ВС ∥ AD – трапеція. Тоді ЕF ∥ AD - теорема 5.4.