23. Вправи для повторення курсу геометрії 10 класу » 23.49

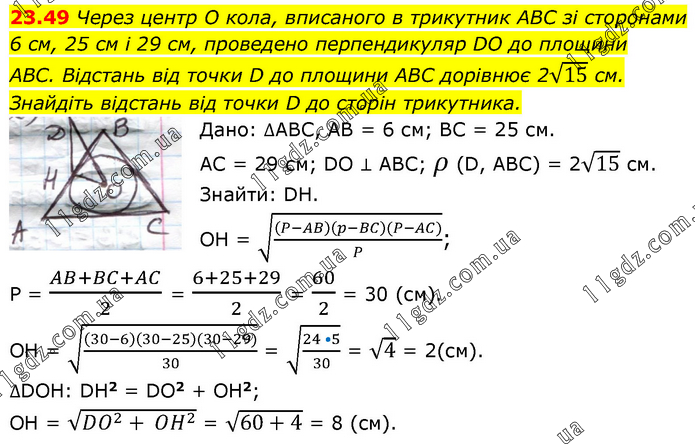
Через центр O кола, вписаного в трикутник ABC зі сторонами 6 см, 25 см і 29 см, проведено перпендикуляр DO до площини ABC. Відстань від точки D до площини ABC дорівнює 2√15 см. Знайдіть відстань від точки D до сторін трикутника. Дано: ∆АВС, АВ = 6 см; ВС = 25 см. АС = 29 см; DO ⊥ ABC; ρ (D, ABC) = 2√15 см. Знайти: DH. OH = √(((P-AB)(p-BC)(P-AC))/P); P = (AB+BC+AC)/2 = (6+25+29)/2 = 60/2 = 30 (см). ОН = √(((30-6)(30-25)(30-29))/30) = √((24 •5)/30) = √4 = 2(см). ∆DOH: DH2 = DO2 + OH2; OH = √(DO^2+ OH^2 ) = √(60+4) = 8 (см).