§ 4. Паралельність у просторі » 30.15

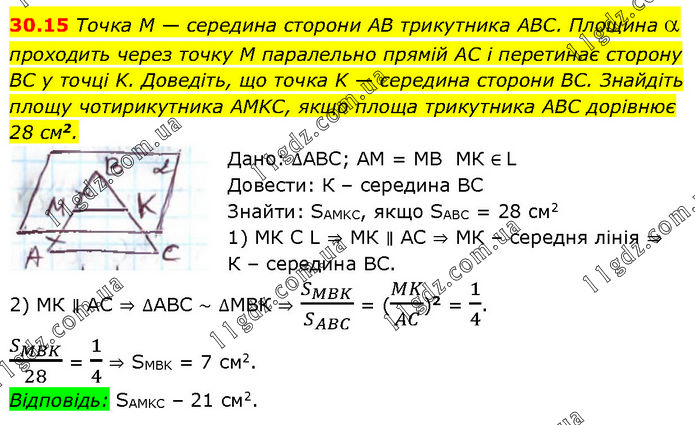
Точка M — середина сторони AB трикутника ABC. Площина  проходить через точку M паралельно прямій AC і перетинає сторону BC у точці K. Доведіть, що точка K — середина сторони BC. Знайдіть площу чотирикутника AMKC, якщо площа трикутника ABC дорівнює 28 см2. Дано: ∆АВС; АМ = МВ МК ∈ L Довести: К – середина ВС Знайти: SAMKC, якщо SABC = 28 cм2 1) МК С L ⇒ МК ∥ АС ⇒ МК – середня лінія ⇒ К – середина ВС. 2) МК ∥ АС ⇒ ∆АВС ~ ∆МВК ⇒ S_MBK/S_ABC = (MK/AC)2 = 1/4. S_MBK/28 = 1/4 ⇒ SMBK = 7 см2. Відповідь: SAMKC – 21 см2.