§ 4. Геометричні фігури та величини » 860

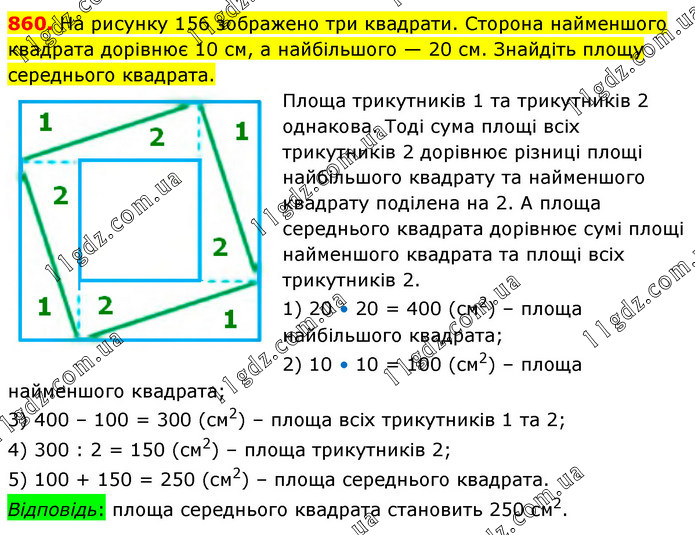
На рисунку 156 зображено три квадрати. Сторона найменшого квадрата дорівнює 10 см, а найбільшого — 20 см. Знайдіть площу середнього квадрата. Площа трикутників 1 та трикутників 2 однакова. Тоді сума площі всіх трикутників 2 дорівнює різниці площі найбільшого квадрату та найменшого квадрату поділена на 2. А площа середнього квадрата дорівнює сумі площі найменшого квадрата та площі всіх трикутників 2. 1) 20 • 20 = 400 (см2) – площа найбільшого квадрата; 2) 10 • 10 = 100 (см2) – площа найменшого квадрата; 3) 400 – 100 = 300 (см2) – площа всіх трикутників 1 та 2; 4) 300 : 2 = 150 (см2) – площа трикутників 2; 5) 100 + 150 = 250 (см2) – площа середнього квадрата. Відповідь: площа середнього квадрата становить 250 см2.